图连通性（一）：Tarjan算法求解有向图强连通分量

Note: 本文最初于 2011年01月27日 星期四 20:32 在 hi.baidu.com/lydrainbowcat 发表。šš

参考文献：http://www.byvoid.com/blog/scc-tarjan/

[有向图强连通分量]

在有向图G中，如果两个顶点间至少存在一条路径，称两个顶点强连通(strongly connected)。如果有向图G的每两个顶点都强连通，称G是一个强连通图。非强连通图有向图的极大强连通子图，称为强连通分量(strongly connected components)，简记为SCC。

下图中，子图{1,2,3,4}为一个强连通分量，因为顶点1,2,3,4两两可达。{5},{6}也分别是两个强连通分量。

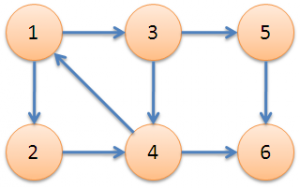
直接根据定义，用双向遍历取交集的方法求强连通分量，时间复杂度为O(N^2+M)。更好的方法是Kosaraju算法或Tarjan算法，两者的时间复杂度都是O(N+M)。本文介绍的是Tarjan算法。

[Tarjan算法]

Tarjan算法是基于对图深度优先搜索的算法，每个强连通分量为搜索树中的一棵子树。搜索时，把当前搜索树中未处理的节点加入一个堆栈，回溯时可以判断栈顶到栈中的节点是否为一个强连通分量。

定义DFN(u)为节点u搜索的次序编号(时间戳)，LOW(u)为u或u的子树能够追溯到的最早的栈中节点的次序号。

对于树枝边(u,v)，有low[u]=min(low[u],low[v]).

对于后向边(u,v) (指向在当前栈中节点的边)，有low[u]=min(low[u],dfn[v]).

当DFN(u)=LOW(u)时，以u为根的搜索子树上所有节点是一个强连通分量。

接下来是对算法流程的演示。

从节点1开始DFS，把遍历到的节点加入栈中。搜索到节点u=6时，DFN[6]=LOW[6]，找到了一个强连通分量。退栈到u=v为止，{6}为一个强连通分量。

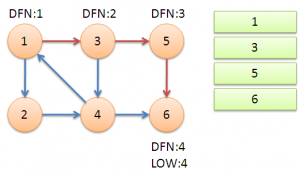
返回节点5，发现DFN[5]=LOW[5]，退栈后{5}为一个强连通分量。

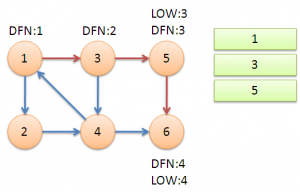
返回节点3，继续搜索到节点4，把4加入堆栈。发现节点4向节点1有后向边，节点1还在栈中，所以LOW[4]=1。节点6已经出栈，(4,6)是横叉边，返回3，(3,4)为树枝边，所以LOW[3]=LOW[4]=1。

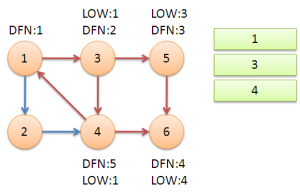
继续回到节点1，最后访问节点2。访问边(2,4)，4还在栈中，所以LOW[2]=DFN[4]=5。返回1后，发现DFN[1]=LOW[1]，把栈中节点全部取出，组成一个连通分量{1,3,4,2}。

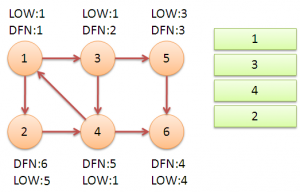
至此，算法结束。经过该算法，求出了图中全部的三个强连通分量{1,3,4,2},{5},{6}。

可以发现，运行Tarjan算法的过程中，每个顶点都被访问了一次，且只进出了一次堆栈，每条边也只被访问了一次，所以该算法的时间复杂度为O(N+M)。

求有向图的强连通分量还有一个强有力的算法，为Kosaraju算法。Kosaraju是基于对有向图及其逆图两次DFS的方法，其时间复杂度也是O(N+M)。与Trajan算法相比，Kosaraju算法可能会稍微更直观一些。但是Tarjan只用对原图进行一次DFS，不用建立逆图，更简洁。在实际的测试中，Tarjan算法的运行效率也比Kosaraju算法高30%左右。此外，该Tarjan算法与求无向图的双连通分量(割点、桥)的Tarjan算法也有着很深的联系。学习该Tarjan算法，也有助于深入理解求双连通分量的Tarjan算法，两者可以类比、组合理解。

求有向图的强连通分量的Tarjan算法是以其发明者Robert Tarjan命名的。Robert Tarjan还发明了求双连通分量的Tarjan算法，以及求最近公共祖先的离线Tarjan算法，在此对Tarjan表示崇高的敬意。

var
 n,m,i,j,x,y,z:longint;
 a,b:array[0..1000,0..1000]of longint;//图
 dfn,low,s:array[0..1000]of longint;//dfn为时间戳，low为祖先，s为栈
 vis,ins:array[0..1000]of boolean;//vis为是否访问，ins为是否在栈中
 num,p:longint;
function min(x,y:longint):longint;
 begin
  if x<y then exit(x) else exit(y);
 end;
procedure tarjan(u:longint);
 var
  i,v:longint;
 begin
  inc(num);//给定一个时间戳
  dfn[u]:=num;
  low[u]:=num;
  vis[u]:=true;
  inc(p);//入栈
  s[p]:=u;
  ins[u]:=true;
  for i:=1 to b[u,0] do
   if not vis[b[u,i]] then//未被访问
    begin
     tarjan(b[u,i]);
     low[u]:=min(low[u],low[b[u,i]]);//是树枝边，取两个low的min值
    end
   else if ins[b[u,i]] then//在栈中
    low[u]:=min(low[u],dfn[b[u,i]]);//非树枝边，去low与dfn的min值
  if dfn[u]=low[u] then//已经找到一个强连通分量
   repeat
    v:=s[p];
    write(v,' ');
    ins[v]:=false;
    dec(p);
    if u=v then writeln;
   until u=v;
 end;
begin
 readln(n,m);
 for i:=1 to m do//构图
  begin
   readln(x,y);
   inc(b[x,0]);
   b[x,b[x,0]]:=y;
  end;
 tarjan(1);
end.